2020年産業医科大学入試問題の微分方程式をPythonで解いてみた

Pythonで微分方程式を解く練習をするために2020年産業医科大学の入試問題で出題された微分方程式を解いてみました。

問題

\(\displaystyle \frac{dy}{dx} + y = 0\)および\(f(1) = 1\)に対して、\(f(0)\)は何か？

数学的解法

$$\frac{dy}{dx} + y = 0$$より$$\frac{dy}{dx} =- y $$

$$\frac{dy}{y} =-dx $$積分して

$$\int \frac{dy}{y} =-\int dx $$

$$\ln|y| = -x+C$$

$$y = Ae^{-x}$$

\(f(1) = 1\)より\(A=e\)なので

$$y = e^{1-x}$$

よって\(f(0)=e\)になります。

Pythonによる数値的解法

ソースコード

ソースコードは以下のようになっています。

import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt

def func(y,x):
    dydx = -y
    return dydx

y0 = 1
x = np.arange(1,-1,-0.01) #1から-1まで0.01ずつ減る

y = odeint(func,y0,x) #微分方程式を解く

plt.plot(x,y) #グラフの作成

plt.show() #グラフの表示

出力結果

出力結果は下のようになりました。数学的解法で解いたのと同じようなそれっぽいグラフが得られました笑。

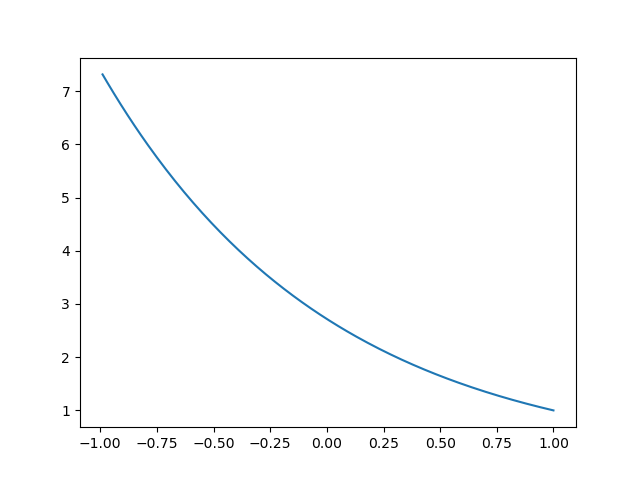
odeintについて考察

odeintを使って微分方程式を解いてみましたが今回はこれだけでは終わりません。

odeintがどのようにして微分方程式を解いているのか考察してみようと思います。

注目するのはソースコードの下の部分です。

def func(y,x):
    dydx = -y
    return dydx

y0 = 1
x = np.arange(1,-1,-0.01) #1から-1まで0.01ずつ減る

y = odeint(func,y0,x) #微分方程式を解く

odeintの処理部分はどのようになっているのか考えてみました。

おそらく下のような順番で処理を行っていると思います。

1. 初期値としてy0=1, x=1を格納（x=1はNumPyリストのx[0]のこと）
2. y, xをfuncに代入
3. dydx=-1を取得
4. y1=y0+dydx\(\times\)(-0.01)=1+(-1)\(\times\)(-0.01)=1.01（-0.01はxの変化分）
5. y1=1.01, x=0.99をfuncに代入
6. 繰り返す

一般化して書くと、

$$y_{n+1}=y_n+\mathrm{func} (y_n,x_n)\times (x_{n+1}-x_n)$$

この繰り返し計算によってyを計算しているのかなと思います。

微分の定義の式で

$$f'(x)=\frac{f(x +\Delta x)-f(x)}{\Delta x}$$

という式があります。変形して

$$f(x +\Delta x)=f(x)+f'(x)\times \Delta x$$

と出来ますからこれをもとにyを次々と計算出来ますね。

次は2階微分方程式をodeintで解こうと思います。