Pythonで微分方程式を解く練習として、ばねの減衰振動の2階微分方程式を解いてみました。
アニメーションで表示する練習もしました。
目標
減衰振動の2階微分方程式をPythonのodeintで解いて、グラフとアニメーションで表示する。
物理学の式
空気抵抗を考慮した時のばねに繋がれた小球の振動を表す運動方程式は以下のようになる。
$$ma=-Kx-kv$$
ただし\(m\)は質量、\(K\)はばね定数、\(k\)は空気抵抗係数を表す。
式を書き換える。
$$ma+kv+Kx=0$$
$$a+\frac{k}{m}v+\frac{K}{m}x=0$$
$$x”+\frac{k}{m}x’+\frac{K}{m}x=0$$
普通は上の式で\(\frac{k}{m}\)を\(2\gamma\)、\(\frac{K}{m}\)を\({\omega_0}^2\)と置くらしいが、今回はソースコードでいじりやすいように下の式のようにした。
$$x”+rx’+wx=0$$
ソースコード
ソースコードを以下に貼り付けます。ソースコードはアニメーションを表示する場合のもので、グラフを表示させたい場合は「グラフの作成」と「グラフの表示」の行をインラインにしてください。
import numpy as np
from scipy.integrate import odeint
import matplotlib.pyplot as plt
import matplotlib.animation as animation
r=0.2
w=2
def func(X,t):
dXdt=[X[1],-r*X[1]-w*X[0]]
return dXdt
X0 = [1,0]
t = np.arange(0,40,0.01)
X = odeint(func,X0,t) #微分方程式を解く
#plt.plot(t,X[:,0]) #グラフの作成
#plt.show() #グラフの表示
#以下アニメーションで表示する場合
fig = plt.figure()
ims = []
frames = 100
for i in range(0,4000,int(len(t)/frames)):
y = 0
x = X[i,0]
im = plt.plot(x,y,color='b',marker='o',markersize=10)
ims.append(im)
ani = animation.ArtistAnimation(fig,ims)
plt.show()出力結果
初期値は、\(x=1, v=0\)としました。定数の設定に関しては\(r=0.2, w=2\)と設定しました。定数の数値に意味はありませんが、\(r\)を大きくすると、はやく減衰するようになり、\(w\)を大きくすると振動の回数が多くなります。
グラフ
横軸が時間\(t\)、縦軸が位置\(x\)を表しています。グラフ内に軸を表示させるの面倒くさかったので本文に書きます笑。
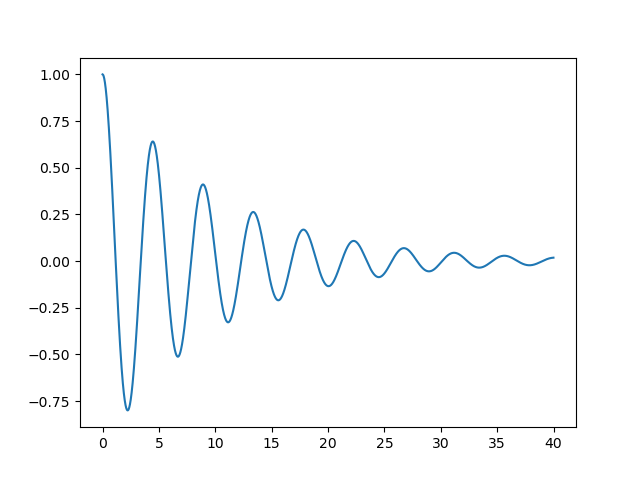
なかなか映えるグラフを得ることが出来ました。しっかりと減衰している様子が分かります。定数を色々変えて遊んでみてください。
アニメーション
アニメーションを作成する際にはこちらのサイトを参考にさせていただきました。ありがとうございました。
まとめ
減衰振動の微分方程式をPythonで数値的に解くことが出来ました。アニメーションで表示することも出来ました。次は電磁気学のローレンツ力を使った3次元の微分方程式でも解いてみようと思います。


コメント