
高校に入学し、数学Aの確率の知識が全然ない時に教師から次のような問題を出された覚えがあります。
「40人のクラスで同じ誕生日の人がいる確率はどのくらいだと思う?」
私は、経験的にあまり同じ誕生日の人に出会ったことがなかったので、5%ぐらいかなと思っていました。
しかし正解の確率はかなり高いのでした。
今回は実際に確率の知識を使って計算してみたいと思います。
目標
\(n\)人のクラスで同じ誕生日の人が存在する確率を求める。
ここでいう「同じ誕生日の人が存在する」とは、「誕生日が1月1日の人から順に挙手をしていったときに、同時に挙手をする人がいる」ということを意味します。
計算式
確率の問題で「存在する」という言葉が出たら、余事象を考えますよね。
「\(n\)人のクラスで同じ誕生日の人が存在する」の否定は「\(n\)人のクラスでみんな誕生日が異なる」になります。
「みんな違ってみんないい」のパターンですね笑。
それでは「\(n\)人のクラスでみんな誕生日が異なる」の全事象は、1人1人365通りの誕生日の可能性があるので、\(365^n\)通りになります。
その中で、「みんな誕生日が異なる」のは、1人目は365通り、2人目は364通り、・・・となるので\(_{365}P_n\)通りとなります。
よって、
$$(n人のクラスでみんな誕生日が異なる確率) $$
$$= \frac{_{365}P_n}{365^n}$$
となるので、
$$(n人のクラスで同じ誕生日の人が存在する確率)$$
$$=1-\frac{_{365}P_n}{365^n}$$
となり、求めることが出来ました。
\(n=40\)の場合
\(n=40\)の場合で計算しますが、電卓では無理なので、Excelで計算しました。
$$1-\frac{_{365}P_{40}}{365^{40}}=0.8912…$$
なんと約90%になりました!
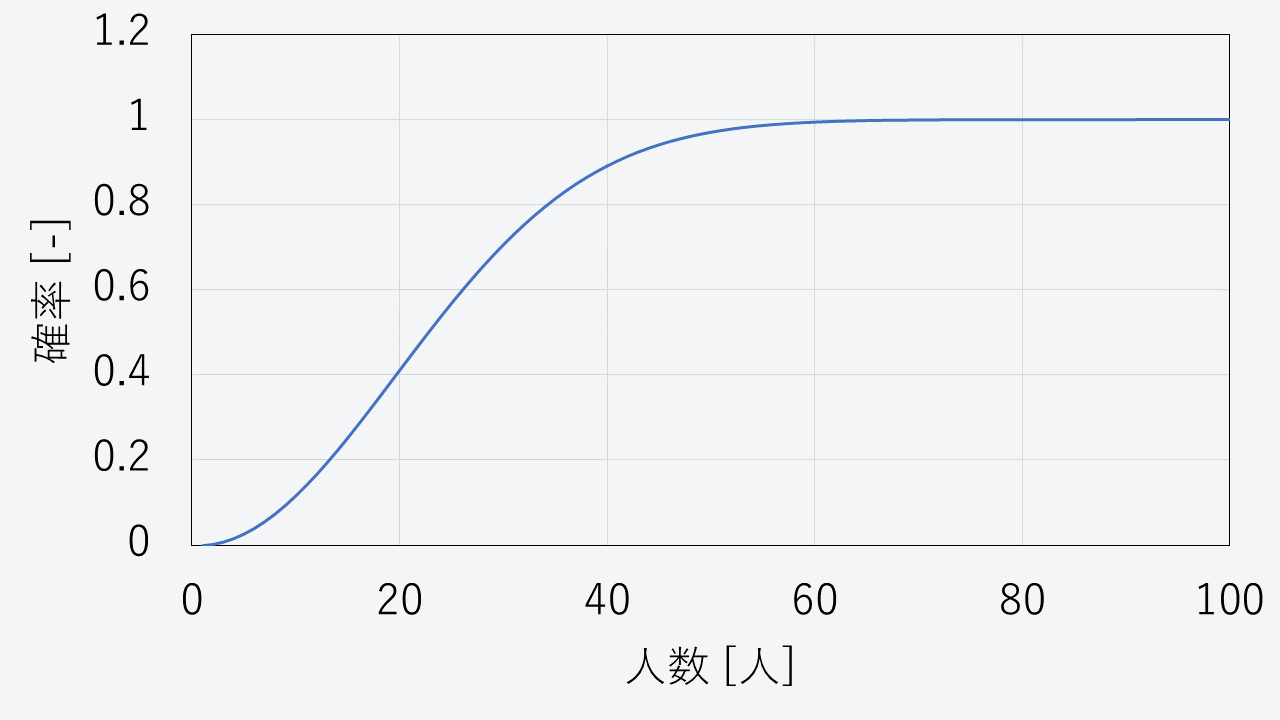
ちなみに\(n\)を変化させた場合の確率の変化は下のようになりました。
10人から20人に増えたところと、20人から30人に増えたところで急に確率も大きくなっていますね。
| \(n\)[人] | \(p\)[-] |
| 10 | 0.116948 |
| 20 | 0.411438 |
| 30 | 0.706316 |
| 40 | 0.891232 |
| 50 | 0.970374 |
| 60 | 0.994123 |
| 70 | 0.99916 |
| 80 | 0.999914 |
| 90 | 0.999994 |
| 100 | 1 |
まとめ
\(n\)人のクラスで同じ誕生日の人が存在する確率を求めることが出来ました。
しかし、計算結果は予想より高いものになりましたが、あまり実感は湧きませんでした笑。


コメント