【中学数学】直角三角形3:4:5以外に知ってる？

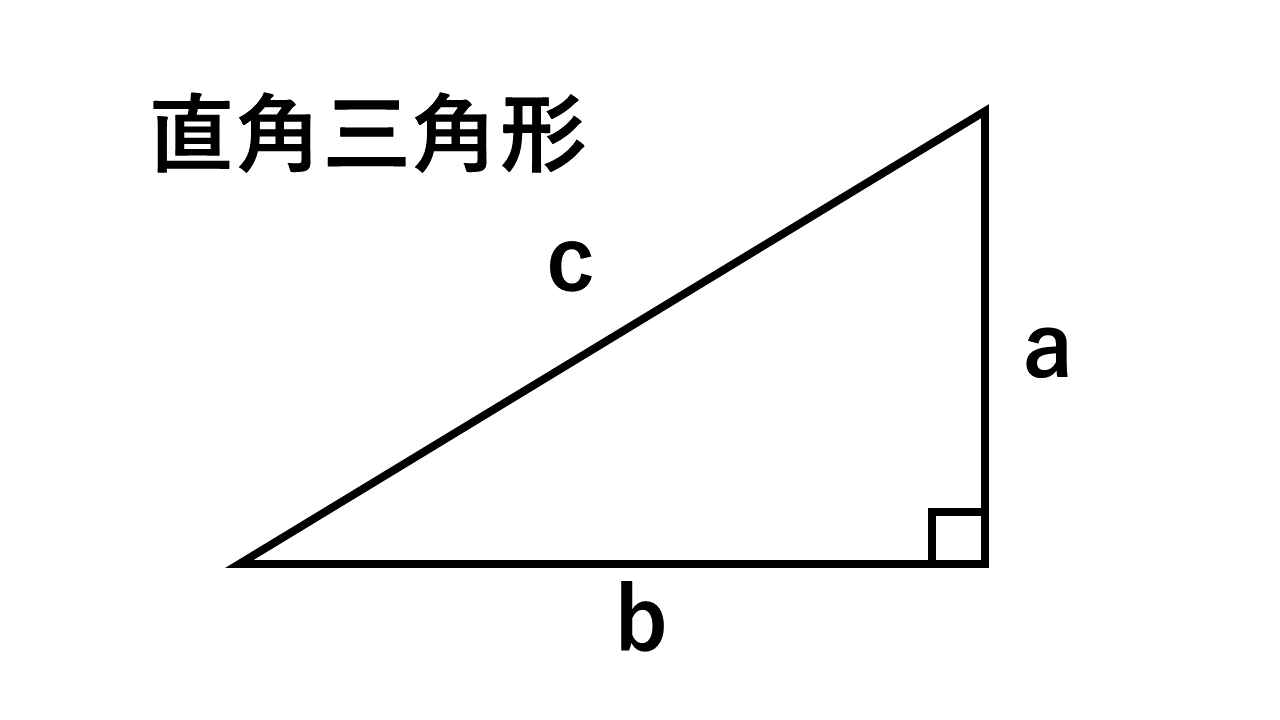
中学校で習う三平方の定理。代表的な直角三角形は3:4:5の直角三角形ですが、他に整数比になる直角三角形を知っていますか？今回は、整数比になる直角三角形を導出したいと思います。

これを変形していきます。

$$c^2 = a^2 + b^2$$

移項して

$$\begin{array}{}
a^2 &=& c^2 \,- \,b^2 \\
a^2 &=& (c + b)(c \,- \,b)
\end{array}$$

ここでaを素数pだとすると

$$p^2 = (c + b)(c \,- \,b)$$

pは素数かつ(c + b) > (c – b)なので

$$\left\{
\begin{array}{}
c + b = p^2 \\
c\,-\,b = 1
\end{array}
\right.$$

bとcに関する連立方程式を解いて、

$$\left\{
\begin{array}{}
b = \frac{p^2 – 1}{2} \\
c = \frac{p^2 + 1}{2}
\end{array}
\right.$$

よって直角三角形の3辺は

$$(a, \,b, \,c) = (p, \,\frac{p^2 – 1}{2}, \,\frac{p^2 + 1}{2})$$

になりますが、これはpが奇数としても成り立ちます。

短辺が99までの直角三角形の辺をPythonに計算させたのでコードと出力結果を載せます。

コード

p = int(input('3以上奇数を入れてね→'))
print('短辺が',p,'までの直角三角形の整数3辺の組を求めます')

last = int((p-1)/2)

for i in range(1,last+1):
  a = 2*i+1
  x = (a, int((a**2 -1)/2), int((a**2+1)/2))
  print('(a, b, c) = ',x)

出力結果：99を入れた場合

3以上奇数を入れてね→99
短辺が 99 までの直角三角形の整数3辺の組を求めます
(a, b, c) =  (3, 4, 5)
(a, b, c) =  (5, 12, 13)
(a, b, c) =  (7, 24, 25)
(a, b, c) =  (9, 40, 41)
(a, b, c) =  (11, 60, 61)
(a, b, c) =  (13, 84, 85)
(a, b, c) =  (15, 112, 113)
(a, b, c) =  (17, 144, 145)
(a, b, c) =  (19, 180, 181)
(a, b, c) =  (21, 220, 221)
(a, b, c) =  (23, 264, 265)
(a, b, c) =  (25, 312, 313)
(a, b, c) =  (27, 364, 365)
(a, b, c) =  (29, 420, 421)
(a, b, c) =  (31, 480, 481)
(a, b, c) =  (33, 544, 545)
(a, b, c) =  (35, 612, 613)
(a, b, c) =  (37, 684, 685)
(a, b, c) =  (39, 760, 761)
(a, b, c) =  (41, 840, 841)
(a, b, c) =  (43, 924, 925)
(a, b, c) =  (45, 1012, 1013)
(a, b, c) =  (47, 1104, 1105)
(a, b, c) =  (49, 1200, 1201)
(a, b, c) =  (51, 1300, 1301)
(a, b, c) =  (53, 1404, 1405)
(a, b, c) =  (55, 1512, 1513)
(a, b, c) =  (57, 1624, 1625)
(a, b, c) =  (59, 1740, 1741)
(a, b, c) =  (61, 1860, 1861)
(a, b, c) =  (63, 1984, 1985)
(a, b, c) =  (65, 2112, 2113)
(a, b, c) =  (67, 2244, 2245)
(a, b, c) =  (69, 2380, 2381)
(a, b, c) =  (71, 2520, 2521)
(a, b, c) =  (73, 2664, 2665)
(a, b, c) =  (75, 2812, 2813)
(a, b, c) =  (77, 2964, 2965)
(a, b, c) =  (79, 3120, 3121)
(a, b, c) =  (81, 3280, 3281)
(a, b, c) =  (83, 3444, 3445)
(a, b, c) =  (85, 3612, 3613)
(a, b, c) =  (87, 3784, 3785)
(a, b, c) =  (89, 3960, 3961)
(a, b, c) =  (91, 4140, 4141)
(a, b, c) =  (93, 4324, 4325)
(a, b, c) =  (95, 4512, 4513)
(a, b, c) =  (97, 4704, 4705)
(a, b, c) =  (99, 4900, 4901)

5:12:13や7:24:25までは知っている人もいるかもしれませんが、それ以上はなかなか知らないと思います。学校の友達に自慢してみてね笑。