はじめに
統計検定の勉強をしていて下のような不偏分散の式を見かけます。
不偏分散
$$s=\displaystyle \sum_{i=1}^n \displaystyle \frac{(x_i-\bar{x})^2}{n-1}$$
なぜ\(n\)ではなく\(n-1\)で割るのかをまとめました。
導出
まず、不偏分散とは、「期待値が真の値に一致する分散」のことです。
じゃあ、\(n\)で割った分散の期待値は真の値(母分散)に一致しないのか?と思いました。
では、\(n\)で割った時の標本分散の期待値を地道に計算してみます。
\(n\)で割った時の標本分散は\( \displaystyle \sum_{i=1}^n \displaystyle \frac{(x_i-\bar{x})^2}{n} \)で表されるので、
\(E\left[ \displaystyle \sum_{i=1}^n \displaystyle \frac{(x_i-\bar{x})^2}{n} \right]\)
\(=\displaystyle \frac{1}{n}E \left[ \displaystyle \sum_{i=1}^n (x_i-\bar{x})^2 \right] \)
\(=\displaystyle \frac{1}{n} E \left[ \displaystyle \sum_{i=1}^n (x_i^2-2x_i\bar{x}+\bar{x}^2) \right] \)
\( =\displaystyle \frac{1}{n} E \left[ \displaystyle \sum_{i=1}^n x_i^2-2 \displaystyle \sum_{i=1}^n x_i\bar{x}+ \displaystyle \sum_{i=1}^n \bar{x}^2 \right] \)
\(=\displaystyle \frac{1}{n} E \left[ \displaystyle \sum_{i=1}^n x_i^2-n\bar{x}^2\right]\)
ここで、
\(E\left[\displaystyle \sum_{i=1}^n x_i^2 \right]\)
\( =\displaystyle \sum_{i=1}^n E\left[X_i^2 \right]\)
\( =\displaystyle \sum_{i=1}^n E\left[X^2 \right] \)
\(= \displaystyle \sum_{i=1}^n (\sigma^2+\mu^2)\)
\(=n\sigma^2+n\mu^2\)
\( E\left[ \bar{x}^2 \right] \)
\(= E\left[ \left(\displaystyle \frac{x_1+\cdots +x_n}{n} \right)^2 \right] \)
\(=\displaystyle \frac{1}{n^2} E\left[\displaystyle \sum_{i=1}^n x_i^2+ 2 \displaystyle \sum_{i<j}^n x_ix_j\right] \)
\( =\displaystyle \frac{1}{n^2} \left( (n\sigma^2+n\mu^2)+n(n-1)\mu^2 \right)\)
\(=\displaystyle \frac{\sigma^2}{n}+\mu^2\)
以上より、
\( \displaystyle \frac{1}{n} E \left[ \displaystyle \sum_{i=1}^n x_i^2-n\bar{x}^2\right] \)
\(=\displaystyle \frac{n-1}{n} \sigma^2\)
\(n\)で割った時の標本分散の期待値を計算すると、\(\sigma^2\)に一致しませんでした。
\( E\left[ \displaystyle \sum_{i=1}^n \displaystyle \frac{(x_i-\bar{x})^2}{n} \right ]\)\(= \displaystyle \frac{n-1}{n} \sigma^2 \)
が成り立っているため、
\( \sigma^2 \) \(= E\left[ \displaystyle \sum_{i=1}^n \displaystyle \frac{(x_i-\bar{x})^2}{n-1} \right ]\)
が成り立ちます。
よって以下の式の説明がつきました。
不偏分散
$$s=\displaystyle \sum_{i=1}^n \displaystyle \frac{(x_i-\bar{x})^2}{n-1}$$
別解
下のような変形が出来ればもっと楽に解けたと思います。
\(\displaystyle \sum_{i=1}^n (x_i-\bar{x})^2\)
\( =\displaystyle \sum_{i=1}^n ((x_i-\mu)-(\bar{x}-\mu))^2 \)
\(= \displaystyle \sum_{i=1}^n ( (x_i-\mu) ^2\)\( +(\bar{x}-\mu)^2 \)\( -2(x_i-\mu)(\bar{x}-\mu))\)
\( = \displaystyle \sum_{i=1}^n (x_i-\mu) ^2\)\(-n(\bar{x}-\mu)^2\)
ぜひこの方法でもやってみてください。

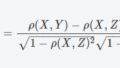

コメント