はじめに
まず、確率変数が3つ\(X,Y,Z\)があるとします。
そして\(XとZ、YとZ\)にはそれぞれ正の相関があるとします。
この時、\(XとY\)は互いに無関係な確率変数だったとしても、\(XとY\)の間には何かしらの相関があるように見えてしまいます。
そこで、\(XとY\)の相関関係から\(Z\)の効果を除いて補正した偏相関係数というものが、下の式で計算されます。
偏相関係数
$$\rho(X,Y|Z)$$
$$=\displaystyle \frac{\rho(X,Y)- \rho(X,Z) \rho(Y,Z) }{\sqrt{1- \rho(X,Z)^2 }\sqrt{1- \rho(Y,Z)^2 }}$$
この式の導出をしたのでまとめます。
導出
まずは、\(XからZ\)の効果を除くことから始めましょう。
\(XとZ\)には相関があり、\(x=a+bz\)の回帰直線を引くことが出来ます。
回帰直線の切片と傾きは、回帰直線による予測値と実測データの差の2乗の合計\(S\)を用いて、導出出来ます。
\(S=\displaystyle \sum_{i=0}^n (a+bz_i-x_i)^2\)
として、
\(\displaystyle \frac{\partial S}{\partial a}=0\)かつ\(\displaystyle \frac{\partial S}{\partial b}=0\)とすることで、
傾き\(b=\displaystyle \frac{\sigma_{xz}}{\sigma_z^2}\)が得られます。
ここは今回のメインではないため、詳しい証明は省略します。
さて、「\(XからZ\)の効果を除く」とは、「 \(X\)から\(Z\)が含まれる項を引く」ということです。
上で計算した\(b \)を\(b_{xz}\)とすると、
\(x=a+bz\)のとき、両辺から\(b_{xz}z\)を引くと、\(x-b_{xz}z=a\)となり、\(X-b_{xz}Z\)は\(XからZ\)の効果を除いた式ということになります。
その確認として、引き算した後の\(x-b_{xz}z=a(定数)\)と\(z\)の相関係数は\(0\)となります。
同様に\(b_{yz}= \displaystyle \frac{\sigma_{yz}}{\sigma_z^2} \)に対して、\(y-b_{yz}z\)とすることで、\(YからZ\)の効果を除くことが出来ます。
\(XとY\)の偏相関係数とは、\(Z\)の効果を除いた後の相関係数のことなので、\(Z\)の効果を除いた後の\(X,Y\)をそれぞれ\(X’,Y’\)とすると、
\(X’=X-b_{xz}Z\)
\(Y’=Y-b_{yz}Z\)
となります。
これらの相関係数は、
\(\rho(X’,Y’)=\displaystyle \frac{\sigma_{x’y’}}{\sigma_{x’}\sigma_{y’}}\)
で計算出来るので、これを変形計算していけば、\(XとY\)の偏相関係数が導出出来そうです。
まずは、\(X’とY’\)の分散を計算していきます。
\(\sigma_{x’}^2\)
\(=V[X’]\)
\(=V[X-b_{xz}Z]\)
\(=E[(X-b_{xz}Z)^2]-E[X-b_{xz}Z]^2\)
\(=E[X^2]-2b_{xz}E[XZ] \)\( +b_{xz}^2E[Z^2]\)\(-(E[X]^2-2b_{xz}E[X]E[Z]+b_{xz}^2E[Z]^2)\)
\(=\sigma_x^2+b_{xz}^2\sigma_z^2\)\(-2b_{xz}\sigma_{xz}\)
\(b_{xz}= \displaystyle \frac{\sigma_{xz}}{\sigma_z^2} \)を代入して、
\(= \sigma_x^2+\left( \displaystyle \frac{\sigma_{xz}}{\sigma_z^2} \right)^2\sigma_z^2\)\(-2\left( \displaystyle \frac{\sigma_{xz}}{\sigma_z^2} \right)\sigma_{xz} \)
\(=\sigma_x^2-\displaystyle \frac{\sigma_{xz}^2}{\sigma_z^2}\)
\(Y\)についても同様に、
\(\sigma_{y’}^2= \sigma_y^2-\displaystyle \frac{\sigma_{yz}^2}{\sigma_z^2} \)
最後に\(X’とY’\)の共分散を計算します。
\(\sigma_{x’y’}\)
\(=E[X’Y’]-E[X’]E[Y’]\)
\(=E[(X-b_{xz}Z)(Y-b_{yz}Z)] \)\( -E[X-b_{xz}Z]E[Y-b_{yz}Z]\)
\(=E[XY]-b_{yz}E[XZ]-b_{xz}E[YZ] \)\( +b_{xz}b_{yz}E[Z^2]\)\(-(E[X]E[Y] \)\( -b_{yz}E[X]E[Z] \)\( -b_{xz}E[Y]E[Z] \)\( +b_{xz}b_{yz}E[Z]^2)\)
\(=\sigma_{xy}-b_{yz}\sigma_{xz} \)\( -b_{xz}\sigma_{yz} \)\( +b_{xz}b_{yz}\sigma_z^2\)
\(b_{xz}= \displaystyle \frac{\sigma_{xz}}{\sigma_z^2},\) \(b_{yz}= \displaystyle \frac{\sigma_{yz}}{\sigma_z^2}\)を代入して、
\(=\sigma_{xy}-\left( \displaystyle \frac{\sigma_{yz}}{\sigma_z^2} \right)\sigma_{xz} \)\( – \left( \displaystyle \frac{\sigma_{xz}}{\sigma_z^2} \right) \sigma_{yz} \)\( + \left( \displaystyle \frac{\sigma_{xz}}{\sigma_z^2} \right) \left( \displaystyle \frac{\sigma_{yz}}{\sigma_z^2} \right) \sigma_z^2\)
\(=\sigma_{xy}-\displaystyle \frac{\sigma_{xz}\sigma_{yz}}{\sigma_z^2}\)
以上より、
\(\rho(X’,Y’)\)
\(=\displaystyle \frac{\sigma_{x’y’}}{\sigma_{x’}\sigma_{y’}}\)
\(=\displaystyle \frac{ \sigma_{xy}-\displaystyle \frac{\sigma_{xz}\sigma_{yz}}{\sigma_z^2} }{\sqrt{ \sigma_x^2-\displaystyle \frac{\sigma_{xz}^2}{\sigma_z^2} }\sqrt{ \sigma_y^2-\displaystyle \frac{\sigma_{yz}^2}{\sigma_z^2} }}\)
分母分子を\(\sigma_{x}\sigma_y\)で割ることで、下の偏相関係数の公式が導出されました。
偏相関係数
$$\rho(X,Y|Z)$$
$$=\displaystyle \frac{\rho(X,Y)- \rho(X,Z) \rho(Y,Z) }{\sqrt{1- \rho(X,Z)^2 }\sqrt{1- \rho(Y,Z)^2 }}$$
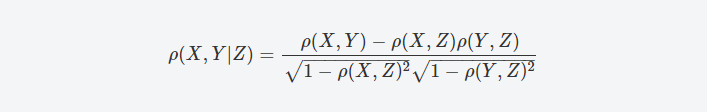

コメント