はじめに
ベイズの定理の式が分かりにくくて、図で理解するとよく理解できたのでまとめます。
ベイズの定理は以下の式です。
ベイズの定理
$$ P(A_i|B)=\displaystyle \frac{P(B|A_i)P(A_i)}{\displaystyle \sum^n_{i=1}P(B|A_i)P(A_i)}$$
ただし、\(A_i\)は互いに排反で\(\displaystyle \sum ^n_{i=1} P(A_i)=1\)を満たし、任意の事象\(B\)について\(P(A_i|B)\)は\(B\)の下での\(A_i\)の条件付き確率である。
図での理解
\(A_i\)は互いに排反で\(\displaystyle \sum ^n_{i=1} P(A_i)=1\)を満たすので、事象\(A_i\)と\(B\)のベン図は下のようになります。
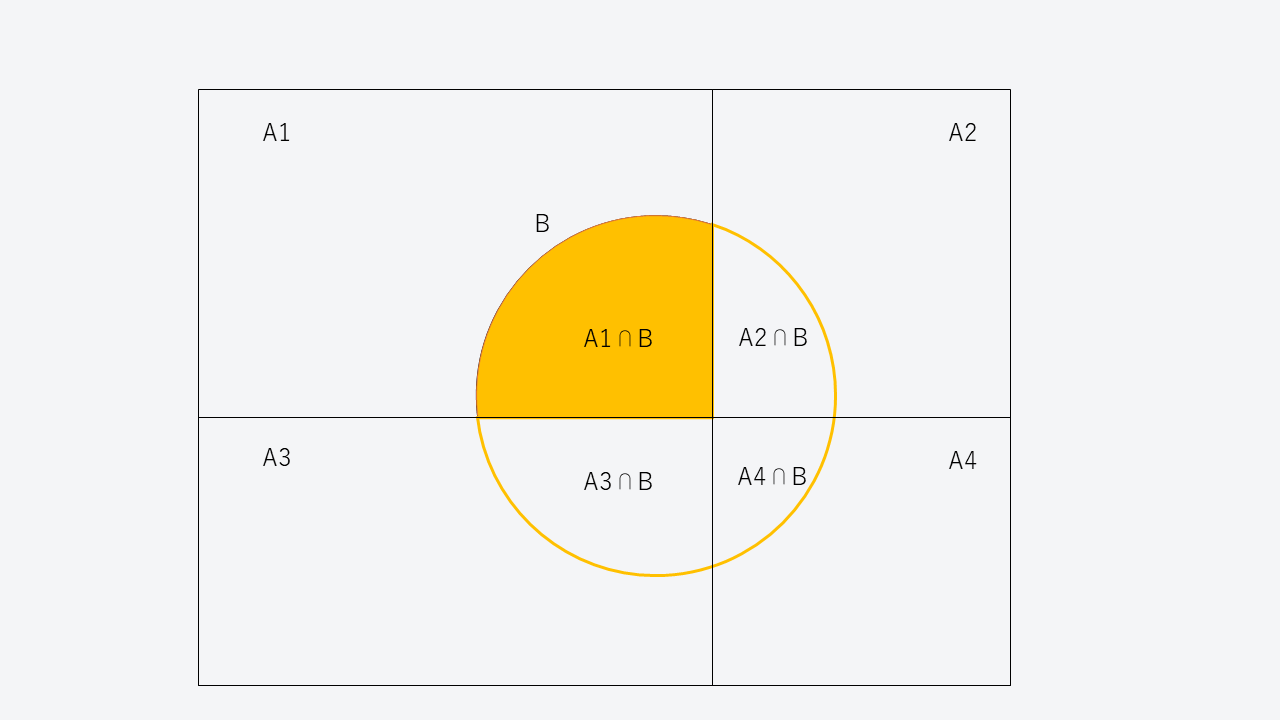
ベイズの定理の左辺\(P( A_i|B )\)は、\(B\)が起きたという条件の下での\(A_i\)が起こる確率です。
\(i=1\)の時、\(P( A_1|B )\)とは、「ベン図の\(B\)の円を確率1として見た時の、オレンジ部分\(A_1\land B\)の割合」を意味します。
面積で考えると下のようになります。
\(P(A_1|B)\)
\(=\displaystyle \frac{オレンジ部分の面積}{円Bの面積}\)
\(=\displaystyle P(A_1\land B) / \{ P(A_1\land B) \) \(+ P(A_2\land B) \) \( + P(A_3\land B) \) \( + P(A_4\land B)\} \)
よって、ベイズの定理は下のような式で書けます。
ベイズの定理
$$ P(A_i|B)=\displaystyle \frac{P(A_i \land B)}{\displaystyle \sum^n_{i=1}P(A_i \land B)}$$
統計検定の問題を解いていますが、この式の方が断然使いやすいです。
この式を使って最初に挙げたベイズの定理を証明する方法は、以下の条件付き確率の式を用いれば簡単に証明出来ますのでよかったら証明してみてください。
$$P(B|A_i)=\displaystyle \frac{P(B \land A_i)}{P(A_i)}$$

コメント